How to compute the dodekatemorion.


Among the Greek papyri, the oldest mention of the dodekatemoria is found in two horoscopes dating back to the 1st century: one already published with translation and commentary in GH;[1] the other found in Oxyrhynchus.[2] In the literary field, the earliest notices of the dodekatemoria are given by Manilius[3] and Manetho.[4]
In P. Lond. 130 the dodekatemoria of the Sun, which is at 14° Aries, and of the Moon, placed at 13° Taurus, are given. According to the horoscope's compiler, the dodekatemoria both of the Sun and of the Moon fall in Scorpio. The authors of GH, on the other hand, who give their (incorrect) calculation procedure on p. 6, believe that both dodekatemoria should fall in Libra: at 2° that of the Sun and at 19° that of the Moon. In the astrological commentary (p. 25) they write: “One has to assume a gross error in the computation of the dodekatemorion.” In our opinion, there is no error, but a misinterpretation of how the calculation should be performed, because of which the sign where the star is located is not taken into account, but the subsequent one.[4*] The result is still wrong, but it is not a mistake. — In P. Oxy. 2555, the dodekatemoria of the Moon (at 19°+½+¹/3+¹/12[5] = 19°55' Capricorn), Sun (at 29°+½+¹/3+¹/12 = 29°55' Taurus), Saturn (at 2°10' Capricorn) and Jupiter (at 23°30' Cancer) are given. Well, the respective dodekatemoria are placed in Leo, Aries, Capricorn and Aries: all correct.
Manilius is the earliest author to inform us that the dodekatemorion is a segment of the ecliptic measuring 2°30' and that each sign contains 12 of them: "Now turn your attention to a minor element to be seen, but of great weight and which can only be designated by a Greek term, dodekatemorion, a definition that explains itself. In fact, since the signs (sidera) all have thirty degrees, [be understood, and the signs are twelve,] conversely the number (30) is divided by two times six; the operation itself shows that in (said) sections there are two and a half degrees"[6]... and we stop here, because if we were to continue, we would have to fill many pages to discuss the many verses of Manilius that are misunderstood and poorly translated. — Manetho, who came a little later than Manilius,[7] does not provide any calculation of the dodekatemorion, but on five occasions he describes its necessary involvement.[8]

Before illustrating the calculation of the dodekatemorion, it seems appropriate to cite some texts that deal with it, starting with the chapter, in which Ptolemy makes a brief mention of it:[9]

1. Some have distributed the regencies (οἰκοδεσποτεῖαι) in even smaller sectors than these (just exposed), calling them 'places' and 'degrees', and assuming as 'place' the twelfth of the twelfth, that is to say 2 and a half degrees, and assigning the lordship (κυρεία) to the signs in succession. Others, then, according to different non-rational placement criteria (κατ’ἄλλας τινὰς ἀλόγους τάξεις), have attributed each 'degree', always from the beginning (of the sign), to each of the stars, in accordance with the placement of the Chaldean districts (ὅρια). 2. Well, we will put aside this type of subdivision (τοῦτο μὲν οὖν), since it is based on an unsound and unnatural line of reasoning; instead, we will take into consideration the other one ((ἐκεῖνο δέ), which is worthy of attention, since it is reasonable to establish the solstitial and equinoctial signs as the beginnings of the dodekatemoria and the districts, and this has been clarified to some extent by those who wrote about it before us, and above all (it is reasonable) because we observe that their natures (φύσεις), powers (δυνάμεις) and coregencies (συνοικειώσεις) originate, in accordance with what has already been explained, from the beginnings of the tropics and the equinoxes and not from anything else, whatever it may be. 3. By setting other beginnings, either we will be forced in the predictions not to consider their natures at all, or, considering them, to fail, having violated and altered the distances of the zodiac that confer to them their own powers.

This is our translation of the text that has come down to us. We must add, so that our Reader is informed, that the most accredited Italian translations, namely that of Feraboli, preferred by professors, and that of Bezza, differ.[10] The problem is not irrelevant.
In this chapter Ptolemy confirms (1) that he is aware of the dodekatemorion of 2 and a half degrees, and (2) that it is attributed to a sign according to the order of the signs. But, since the subdivision described immediately after—the one concerning the individual degrees, the so-called monomoiria—is ἄλογον, that is, an illogical gimmick, it should be noted that this one of 2 and a half degrees is not described as such.[11] The following period contains an antithesis (τοῦτο[12] μὲν... ἐκεῖνο δέ) completely ignored by the translators. We should remember that Ptolemy is very fond of these particles and never uses them at random. Hence, τοῦτο μὲν refers to what immediately precedes, that is, to the subdivision by single degrees, ἐκεῖνο δέ to the subdivision by dodekatemoria. After that Ptolemy seems to allude to the disconnection between the sidereal zodiac and the tropical zodiac. Leaving aside the question of the precession of the equinoxes, let us ask ourselves why Ptolemy mentions it here and not in chapter 10 (Of the seasons of the year)! The translations by Robbins (London 1940) and Feraboli are therefore incomplete and, therefore, incorrect. Ptolemy means that, if the districts, which he refers to for the sake of scruple,[13] and the dodekatemoria were not framed—like the signs of course, but he does not say it—within the solstices and the equinoxes, they would crumble miserably and become completely useless to the art of prediction. Who, then, are these "some (τινες)" who introduced the dodekatemoria, the astronomer does not say.
The Anonymous Commentator holds a completely different opinion, providing details that cannot be gleaned from the Ptolemaic text, so much so that it seems at first glance that he is reading a different text:[14]

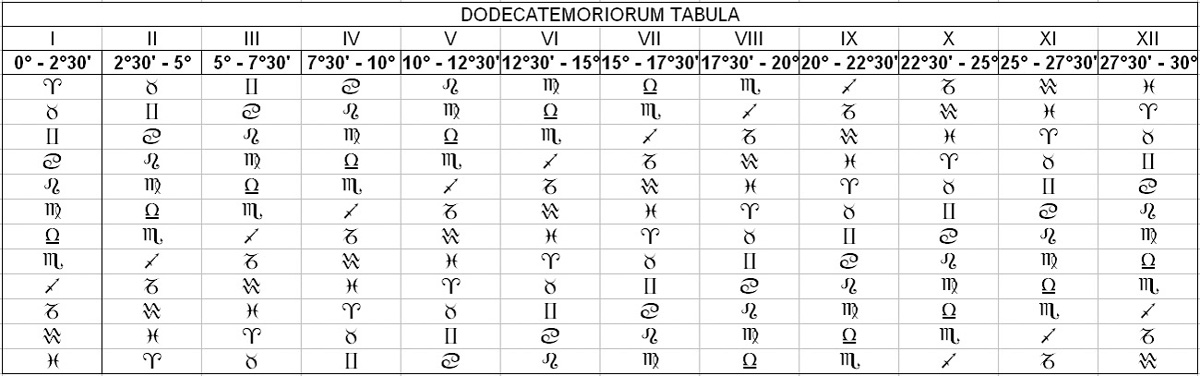
The best teacher is one who not only relates true and just principles, but also discusses false ones that can mislead the mind of a young person; well, the Venerable [scil. Ptolemy] proved himself to be such in his teaching on districts, refuting the false opinions of the Egyptians. And now he wishes to refute other principles of theirs that aim at vanity. In addition to the division of signs into districts, there were also other minor subdivisions among the Egyptians, such as that of dodekatemoria and individual degrees. Lest anyone think that he intends to ignore them, he writes about them in order to refute them as fatuous and aiming only at vainglory.[15] There were therefore such dodekatimoria among them: the degree occupied by a star, they multiplied it by twelve; to each sign they assigned 30 degrees (subtracting them from the total) and where it [scil. the remainder] ended, they said that the dodekatemorion was there. Dorotheus also does the same.[16] He, however, does not do (the multiplication) by twelve, but says that to each sign he assigned 2 degrees and ½ and, where it ended, he said that the dodekatemorion was there. He says (in the end) the same thing as Dorotheus.[17] In fact, the 2 and ½ degrees are analogous to the number 30. If we do 2 × 12, the result will be the number 24, but the 12 added half-degrees complete the number 30. As a proof that (the two calculations) agree, let us take the (first) three degrees of Aries, as Dorotheus says,[18] and, according to Ptolemy, let us give 2½ to Aries.[19] The half degree will be of Taurus, and it will be the 6th degree.[20] And the result is the same with both methods.

What the Anonymous Commentator means can be explained as follows: whether you multiply the degrees by 12 and then subtract 30° as many times as possible, or you divide the sign into sectors of 2 degrees and ½ and check in which sector it ends up in, the result is the same. In fact, 3° Aries × 12 = 36°, I subtract 30°, and remain 6° which fall in the second sign starting from Aries, that is Taurus. Or, by dividing the sign into sectors of 2 and a half degrees, you can note that 3° falls into the second sector: 3° - 2°30' = 30' which, multiplied by 12, gives 6° of the second sector attributed to Taurus.
In the subsequent skolion entitled On Monomoiria (Περὶ μονομοιρίας), to which he devotes only a few lines, the Anonymous Commentator returns to the subject of the dodekatemorion and repeats what he has already said: “They called them dodekatemoria as a result of the division (by 12): in fact, dividing thirty degrees of the zodiac by 12, they gave each sign 2½ degrees; such is, in fact, the width of the twelfth part.” At this point, the text shows itself to be the result of a corrupted reshuffle, as indicated by the previous contradictions. Our translation attempts to render the syntactical inconsistencies of the text: "Others [scil. astrologers] of the past (παλαιοί) by the number 12 * the 5 multiplied, which is the same as 2½ degrees. If you add up the total number of degrees, you complete the 30 degrees of the dodekatemorion. (Ptolemy) made fun of the dodekatemorion and demonstrated, having broken it down into smaller (parts), of 2 particles (μορίων) and a half, of such width in fact results the twelfth of the particle, which those of the past multiplied by 12 for greater clarity.” It is clear that this last part, as rambling as it is, is the result of a clumsy reworking.[21]
So, according to the Anonymous, Ptolemy proves “false all (these) things that the Egyptians approve. In fact, they are neither credible nor natural, that is, they are not true, even if they may seem plausible.[22] Nor does he want to refer to the bare tradition of the dodekatemoria, but he joins to it a necessary small postulate (θεωρημάτιον), this one: the beginnings of what is observed in the zodiac, says, necessarily has its beginning either from the tropics or from the equinoxes: all what has already been demonstrated in this matter, we have reported it, and mainly the astrologers who preceded us (οἱ παλαιοί) testify to these beginnings.” A final consideration follows: “From the above those who have well reflected on dodekatemoria, retort with sagacity: if we find then that the dodekatemorion of Aries has fallen into Virgo, either we use it or not use it. If we do not use it, it has been taken as a useless surplus. If we use it, we can no longer understand the power of Aries, as it was understood from the beginning.”
This is what the Anonymous Commentator devotes to the dodekatemorion. Despite the disastrous condition of the text, we can note the following: he is convinced that Ptolemy considers absurd even the dodekatemoria, and not only the assignment to the planets of the rule on each individual degree; but that is not what is read in the Ptolemaic text. That Ptolemy mocks (διέπαιξε) the dodekatemoria, is a gratuitous opinion. That the authors of such a subdivision are the Egyptians, is taken for granted; but that is not what we read. It is surprising that “the venerable (ὁ παλαιός)" is Ptolemy—and that it is Ptolemy is confirmed by attributing to him the refutation of the Egyptian districts. The skolia of the Anonymous Commentator are usually preceded by a quotation of a phrase or expression from the Ptolemaic text; the mentioned skolion on monomoiria is titled, precisely, Περὶ μονομοιρίας, but the word is never met with in Ptolemy. All this, without forgetting the clear patching up of two versions, nourishes the suspicion that someone else tampered with the Anonymous Commentator's commentary, distorting and expanding the original text. Otherwise, we would be forced to assume that the Ptolemaic text of this chapter would have come to us mutilated and corrupted. We can, in any case, admit that the calculation of the dodekatemorion is the work of the scrupulous Anonymous Commentator, who illustrates it perhaps in opposition to other erroneous procedures, such as that of Paulus of Alexandria, unwisely approved by Neugebauer and van Hoesen.[23]
A second text, which scholars are interested in, is Porphyry's chapter On the Dodekatemorion:[24]

The Moon's dodekatemorion is computed in two ways. First, having observed how many degrees the Moon holds in its sign, divide (its degrees) from that sign by 2½ in succession, and where the number ends, that will be the dodekatemorion. If, for example, the Moon holds the 13th degree of Aries, I will give Aries 2½, Taurus 2½, Gemini 2½, al Cancer 2½, al Leo 2½, and therefore the dodekatemorion will end in Virgo, the house of Mercury. Similarly, the Sun's dodekatemorion is computed in the same way, as is that of the horoscope: when you observe which degree is rising, you will divide by 2½ those that are about to rise.[25]
Some people obtain the dodekatemorion of the Moon in another way. Seeing how many degrees it is distant from the Sun, from these subtract the thirties (you can), and <divide> the remaining degrees by 2½, starting from the sign that the Moon holds (τὰς δὲ λοιπὰς <ἐπιμέριζε> ἀνὰ βL΄, ἀφ’ οὗ ἂν ἐπέχηται ἡ Σελήνη ζῳδίου).[26] If there are no thirties, divide those degrees by 2½. The horoscope, however, must be defined with great accuracy (ἐξακριβουμένους) using tables.[27]

In the first part, Porphyry, who does not appear to be much fond of calculations, gives the correct procedure. In the second, however, without stating the source or offering an example, he reserves special treatment for the dodekatemorion of the Moon, which can be simplified as follows: to the degrees of the Sun, add the degrees between the Moon and the end of the sign (if the result exceeds 30 degrees, subtract them); then divide the remainder by 2½° degrees, and where the number ends, there is the dodekatemorion of the Moon. In substance, with this method the Moon is moved from its former place, which makes no sense either from an astronomical or astrological point of view. In astrology, in fact, no law or figure can exist without being confirmed, even if only by analogy, by observable phenomena. In our opinion, Porphyry either misunderstood his source, or the text underwent an incautious reworking,[28] as can be inferred from the last sentence on the horoscope, which is completely out of context. Feraboli, on the other hand, trusting the editors, does not report any difficulty. In any case, Porphyry confirms the correct calculation.
Along with this one by Porphyry, the 23rd chapter from the Summary (Συγκεφαλαίωσις) of the first book of Antiochus's Preliminary Notions (Εἰσαγωγικά) is cited, presumably as confirmation. The Greek text is also worth mentioning:

κγ'. Καὶ τὸ δωδεκατημόριον δὲ τῆς Σελήνης διχῶς θηρεύεσθαί φησιν, ὅπως τε δεῖ τὸ κλίμα λαμβάνειν κα̥ὶ ὡς τὰ μὲν ὀρθὰ τῶν ζῳδίων ἐν πλείονι, τὰ δὲ πλάγια ἐν ἐλάσσονι ἀναφέρεται.[29]

The only one to translate it, to our knowledge, is Bezza: "The twelfth of the Moon is taken in two ways, since the latitude must be observed: in fact, the straight signs ascend in greater time, the curved signs in less time."[30] A loose rendering which outrages the common sense and the Greek language as well. Our translation sounds differently:

23. And (Antiochus) says [= explains] that the dodekatemorion of the Moon is discovered in two ways, and (he says) how the clima must be assumed, and that [= why] the straight signs ascend in greater time, while the oblique ones in less time.

Here, the epitomizer simply limits himself to reporting the content of chapter 23. In other words, there is nothing that concerns the dodekatemorion, except the citation of the word.
We close the overview with a text attributed to Rhetorius, although the language leaves one in doubt:[31]

18. Of the dodekatemoria of the stars.
The ancients explained the dodekatemoria of the stars in three ways: Paul in his Introduction said to multiply the degrees of the star by 13[32] and from its sign subtract 30 degrees for each sign, and, wherever the number arrives, in that sign is the dodekatemorion of the star. Dorotheus in the 11th book says to multiply the degrees by 12. Ptolemy says in the 26th chapter of the first book to subtract two and a half degrees along the sign (itself). From experience, I have found Dorotheus' method more consistent with that of Ptolemy; and I find myself in greater agreement with these (two) methods, that is, the 12-method and the 2½-one. Thus, in fact, the two methods arrive at the same sign, as in this example: the Moon is at 25° Taurus; multiplying[33] this 12 times, I find 300 degrees, which I release in groups of 30 at a time starting from Taurus, and end up at 30° Aquarius, completing the signs. Or, releasing these 25° Taurus in groups of 2½ at a time, (the calculation) ends in Aquarius, completing the sign of two and a half degrees. If I were to do 25 times 13, the number would end at 25° Pisces, and that would be a big difference. In genitures, the method of the dodekatemoria is a necessary complement: I have also given the effects (which they mean), so that someone does not use them as if they were just an extra.

Here too, the calculation we illustrate below is confirmed. Returning to Ptolemy, who are these 'some'? Today we know, thanks to the publication of some tablets in cuneiform writing, that the dodekatemorion comes directly from the Mesopotamian astrologers, that is, from the Chaldeans![34] Why Ptolemy, who also mentions the Chaldeans, attributes the dodekatemoria generically to 'some,' is at the very least strange. Perhaps, not wanting to attribute their paternity to those same people whose districts he had contested above—even if to a lesser extent than those of the Egyptians—he preferred to remain vague. But it is only a hypothesis without any support. Whoever does not want to admit the dependence of Egyptian astrology on Chaldean astrology, would have to necessarily hypothesize a common source with obvious temporal consequences.

And finally, we come to the calculation of the dodekatemoria. The tablet translated by Pettinato (see note 34) leaves no doubt: "Thirty days correspond to a beru (= 30°). You have to take 2.5 days as a portion, and so you will get 12 portions of the constellation of Aries. Multiply 2°30' by 12 which make up the nucleus of the constellation of Aries and so you get 30° as a result. In 30 days there are 12 segments of the constellation of Aries. First segment: its name is Aries; Second segment: its name is Taurus; [etc.]. Total: 12 segments of the constellation of Aries which the Sun and the Moon pass through. I have shown it to you." It is clearly the teacher who instructs the student on how to divide the remaining zodiac signs to complete the entire 360° circle.
We have prepared the table below, following the instructions of the Mesopotamian astrologer exactly. The Roman numerals in the first line number the columns and the corresponding segments, while in the second line the initial and final degrees of each individual segment are indicated.


And then in the first column all the signs from Aries to Pisces are listed. Since the dodekatemoria of each sign begin, as the tablet says, from the sign itself, each sign indicated in the first column is followed, in order and on the same line, by all the other signs.
Let us start with the example given by the Anonymous Commentator: 3° Aries. Well, from the second line we note that the third degree falls in the second column. On the line that starts from Aries, the relative box of the second column belongs to Taurus, which is the sign where the dodekatemorion of 3° Aries falls. Very simple! As for the degrees we have to multiply 3° × 12 = 36°, and the thirty-sixth degree starting from 0° Aries corresponds to 6° Taurus. But let us take a second example: 11° Virgo. The eleventh degree falls in the fifth column, we go down to cross the box of the line that begins with Virgo, and we will find Capricorn, which is the sign where the dodekatemorion of 11° Virgo falls. As for the degrees, we multiply 11° × 12 = 132°, the one hundred and thirty-second degree starting from 0° Virgo corresponds to 12° Capricorn (150 + 132 = 282); as a counterproof: 11° × 360°: 30° = 132°.
The preposterous distinction between 'zodiacal dodekatemoria' and 'planetary dodekatemoria' was caused by the misunderstanding of the texts, and by the propaganda made by Bouché-Leclercq, author of the famous L'Astrologie Grecque (1899), admired and quoted by all, whose pretentious title should actually be (Comment ridiculiser) l'astrologie grecque (en la traitant à ma façon).[35] Such a distinction between the two types of dodekatemoria is reaffirmed by Baccani[36] and Feraboli.[37] The only one who has understood the problem well is Housman: "I advise no one to read Mr Bouché-Leclercq's account of the matter, the astrol. Grecque pp. 299-303, unless he wants to be confused and misled."[38]
Coming back to the calculation, the only doubtful case is when the result reaches exactly the boundaries of the sectors. The example quoted by Retorio with the Moon at 25° Taurus is a case in point: 300°, in fact, without minutes and/or seconds, can mean 30° Aquarius as well as 0° Pisces; a case that is not impossible, but very improbable.
In conclusion, the principle on which the dodekatemorion is based is given by a very simple analogy:[39] as 30° are to 360°, so the dodekatemorion is to 30°; in fact 30 × 30 : 360 = 2.5. The proof of the correctness of the dodekatemorion is obtained—as we have seen—by multiplying the degrees in the sign × 360, and dividing the result by 30: it must be equal to the degrees in the sign × 12. Any other calculation is to be considered an error.
This analogy, then, gives rise to the following one: as the Moon in 1 month (30 days) travels through the whole zodiac (on average 2 and a half days, 2°30' × 12, per sign), in the same way the Sun in 1 month reviews the 12 dodekatemoria of a sign, that is the whole (micro-)zodiac.

NOTE.

[1] Cf. O. Neugebauer e H.B. van Hoesen, Greek Horoscopes, Philadelphia 1987, p. 21 ff. (P. Lond. 130).

[2] Cf. P. Oxy. XXXI (1966) nr. 2555, p. 83 ff., propounded again by Donata Baccani, Oroscopi greci, Messina 1992, p. 81 ff., without translation.

[3] Cf. Astr. 2,713÷722 [Housman]. It is best to draw a veil over Manilius' Italian edition (Milan 1996) (only Feraboli's contributions are saved, but not entirely). The one edited by Dora Liuzzi in five volumes (Lecce 1995÷1997) is sincere and usable.

[4] Cf. Apotel. 4,165 ss.: Ταῦτα μὲν ὡράων σκεπτήρια· νῦν δέ με χρειὼ | ἀκτινηβολίας ὁρίων τ' αἰθωπὰ κέλευθα | δωδεκατημορίων τ' ἄστρων κυκλόεσσαν ἐνισπεῖν | Ζῳδιακήν... The editor's translation (Jane L. Lightfoot [Oxford 2023]) is the following: «These signs are from the Hours. Now I'll describe Castings of rays, the shining paths of terms, And, of the twelve parts of the stars, the round Zodiacal path», where "of the twelve parts of the stars" will only make sense in the translator's head. Manetho means: “These are the things to be considered at the birthtime; but now it is the right moment to explain the beams cast, the obscure succession of the districts and the cyclical repetition of the dodekatemoria in the zodiac...” While up to v. 164 Manetho spoke of the effects of the various configurations “on those who are born mortals (γεινομένοις θνητοῖσιν)... at the hour of birth (ἐς βίου ὥρην)" (v. 17), which the philologist poorly translates, from v. 165 he intends to explain the effect of the aspects (beams cast), of the districts and of the dodekatemoria. Since he has already spoken of the signs, the association with the districts excludes that Manetho with δωδεκατημόριον meant 'zodiac sign'. The succession of the districts cannot be shining, because they are not visible: αἶθοψ is etymologically connected with αἴθω, 'I burn,' αἰθός, 'dark, brown, parched,' αἰθίοπες, 'dark-faced,' αἰθαλόω, 'I blacken,' etc. As for the expression δωδεκατημόρια (τῶν) ἄστρων, read what Housman writes in Manil. Astr. II, p. xxiv.

[4*] Twelve centuries later, Joannes Camaterus in his Introductio in astronomiam—an astrological poem in verse written in late Greek interspersed with expressions from spoken language, in some cases not immediately comprehensible (ed. Weigl, Leipzig 1908)—proposes a bizarre calculation, in which the sign of the dodekatemorion is found starting from the subsequent sign: "Let the Moon be in Aries at 15 degrees; Multiply the place of the degree - twelve (times) fifteen is one hundred and eighty - paying attention to the twelve signs before the degrees and give each sign in sequence 30°, and [= but] 15° are to be reserved for the sign of the Moon, since the Moon, positioned at 15° Aries, needs (another) 15° to complete the 30° of Aries. For this reason one does not begin with Aries, but with Taurus: give (then) 30° to Taurus, similarly to Gemini, Cancer and Leo, and equally to the rest, (that is) 30° to Virgo; as for Libra (you give them) in this way: (the computed degrees) reach the 15th degree in Libra. Where the counted degrees of the Moon (αἱ τῆς Σελήνης ψῆφοι) come to an end, consider that the dodekatemorion is there" (cf. vv. 3003÷3019). According to Camaterus, therefore, to find the sign, once the degrees of the Moon have been multiplied by 12, 30° are assigned to each sign, starting from the next sign: 180° are equivalent to 6 signs and the sixth sign starting from Taurus is Libra; as for the degree, since the Moon lacks 15° to complete Aries, they are subtracted from Libra and it will thus be found that the dodekatemorion falls in 15° Libra. Another example: Moon at 17° Taurus; 17 × 12 = 204, corresponding to 6 signs + 24°; The sixth sign from Gemini is Scorpio; however, since the Moon lacks 13° to complete Taurus, this must be subtracted from 24°, so the dodekatemorion of the Moon placed at 17° Taurus falls in 11° Scorpio. The calculation is incorrect, but, as in the case of P. Lond. 130, it stems from a misunderstanding, that is, from a failure to understand the underlying principle.

[5] This is our reading of the last fraction; both the editor and Baccani read ι’β’, which makes no sense. Indeed, the iota seems to have an apex, but it must be an oversight; in fact the fraction should be read ¹/10+2! This papyrus is probably the fair copy of the original notes written by the person who drew up the horoscope. This can be deduced from the position of the luminaries, which, despite having different degrees, would have the same minutes; the fractions, in fact, are exactly alike, which is highly improbable. A 'coincidence', therefore, to be ascribed to the copyist.

[6] Cf. Manil. Astr. 2,693÷699.

[7] At the end of the sixth book (see 745 ff.) Manetho provides the data of his birth sky, and it is so clear and precise that it can be dated with ease: he was born on 27 or 28 May of the year 80, Gregorian date. The uncertainty of the exact place and time remains. In fact, if the MC was in Sagittarius (βέλος Κένταυρος ἀνέλκων) and the ascendant in Aquarius, assuming the birth in Alexandria, on May 27 the birth was between 23h24m and 0h13m (local time, LMT), that is between the entry of the MC in Sagittarius and the exit of the ascendant from Aquarius; on May 28, instead, between 23h20m and 0h09m. Obviously, the positions of the planets are the sidereal ones; we have used those according to Lahiri, because they are always the closest to the positions given by Hellenistic astrologers, and often coincide. The authors of GH (v. p. 92), then, confuse Sagittarius with the constellation of the Centaur; and, since it is astronomically impossible that the MC falls in Libra, if the ascendant is in Aquarius, as scholars who have adopted the American typical attitude, they move the ascendant in Capricorn, that is, they attribute their own error to Manetho. Even Lightfoot understood that the constellation has nothing to do with it! Finally, astrological considerations, which we refer to elsewhere, lead us to believe that the most probable date was 28 May.

[8] Cf. Apotel. 4,209.227.250.298.336.

[9] Cf. Tetr. 1,22.

[10] Where Feraboli, for example (cf. Cl. Tolomeo, Le previsioni astrologiche, Milano 41998, p. 90), translates "it is reasonable to make the beginning of the signs coincide with the equinoctial and solstitial points," Bezza (cf. Commento al primo libro della Tetrabiblos, Milano 1990, p. 351) has "it is in fact reasonable to assume the beginnings of the dodekatemoria and the boundaries starting from the equinoctial and solstitial points." This depends in part on the omission of καὶ τὰς τῶν ὁρίων (and those of the districts) in the codd. of group α (Feraboli in the apparatus is confusing) accepted by Robbins (London 1940) and by Feraboli who follows him. Actually, without ὁρίων the preceding δωδεκατημορίων can be understood as 'of the (zodiacal) signs', while the coupling with ὁρίων would require, given the context, to understand 'of the dodekatemoria.' In his adparatus Hübner (Teubner 1998, p. 82) admits to ignoring whether this omission is correct or not.

[11] The phrase "calling them places (τόπους... ὀνομάσαντες)" is somewhat disturbing, since no other source indicates that the 'twelfths of the twelfths' were called 'places'.

[12] The editors read ταῦτα, since τοῦτο is given only by codex V, the most authoritative. The different reading does not change much; however the attention Ptolemy paid to these correlations makes us prefer τοῦτο.

[13] The districts attributed to Ptolemy, in fact, are not his, but those of an anonymous author, found—says the Astronomer—in a worn-out manual, and he speaks of them because they are more coherent than both the Egyptian and Chaldean districts.

[14] Cf. In Claudii Prolemæi Quadripartitum enarrator ignoti nominis, ed. Hieronymus Vuolfius, Basileæ 1559, p. 47 f. On the question of who the translator is, cf. the detailed article by St. Heilen, H. Zäh, Who Edited and Who translated the Anonymous Commentary to Ptolemy's Tetrabiblos and (Ps.-)Prophyry's Isagoge (Basel 1559)?, in “MHNH” 20 (2020), pp. 93-128.

[15] The Ptolemaic text does not allude to vainglory in the slightest: Ptolemy limits himself to saying that the subdivision into individual degrees is illogical.

[16] Cf. Doroth. p. 327, vv. 7÷9 [Pingree], where however the testimony of the Anonymous Commentator is only half cited! In addition to that of the Anonymous Commentator there is also the testimony of Rhetorius (cf. CCAG I, p. 154, v. infra), who mentions the three different calculation procedures used by the astrologers of the past (παλαιοί), including the one, in our opinion erroneous, expounded by Paulus of Alexandria (cf. Elementa apotelesmatica, p. 45 f. [Boer]) and repeated by his commentator Heliodorus (cf. In Paulum Alex. Commentarium, p. 38 f. [Boer], now attributed to Olympiodorus). Hephaestion, as to the calculation procedure, gets it over with in four words (cf. Heph. Theb., Apotelesmatica, p. 42 [Pingree]); elsewhere (p. 234,8 ff.; II, p. 1,20; 47,5; 268,26) he reiterates with the same sentence the importance that the ancients attributed to the dodekatemorion of the horoscope for the purposes of prediction.

[17] We have translated this sentence according to Wolf's Greek text, but it is clearly confusing and contradictory. A slight improvement would be achieved by deleting the sentence "He says the same thing as Dorotheus (ταὐτὸ δὲ φησὶ τῷ Δωροθέῳ)," which repeats the one above: "So does Dorotheus."

[18] That is, multiply them by 12 and subtract 30.

[19] Here the Commentator is saying the opposite of what he said shortly before.

[20] That is, multiply the ½ degree difference by 12.

[21] The text has παρὰ τὸν δώδεκα ἀριθμὸν (by the number 12), followed by 'the 5 multiplied,' which translates a corrupt ἐπολλασίασαν, instead of ἐπολλαπλασίασαν. But in Greek 'I multiply by' you say πολυπλασιάζω (less well πολλαπλασιάζω) ἐπί or εἰς, while 'I divide by' you say μερίζω παρά. In the sentence, however, there is no trace of μερίζω, nor can παρὰ τὸν δώδεκα ἀριθμόν (by the number 12) be supported by ἐπολλαπλασίασαν. Attempting to revise the text without the aid of the manuscript codices would be pointless. We must, therefore, wait for the critical edition that the Spanish Caballero-Sánchez is preparing.

[22] The translation of this last sentence is rather free, because the text is convoluted.

[23] V. GH, p. 6.

[24] Cf. Porphyrii philosophi Introductio in Tetrabiblum Ptolemaei, edd. Aem. Boer et St. Weinstock, in CCAG V.4, p. 210 f.

[25] Porphyry means that, if the horoscope is at 23° Aquarius, the 23 degrees that are about to rise must be divided, certainly not those that have already risen!

[26] Read ἀπὸ τοῦ ζῳδίου, οὗ [an ὃ assimilated to its antecedent] δ’ ἂν ἐπέχηται ἡ Σ.

[27] What value the editor gave to ἐξακριβουμένους (the codd. have ἐξακριβωμένους, which changes nothing), plural accusative of the middle present participle, we cannot imagine; if forced, one might think of an ἐξακριβούμενον as a predicate of ὡροσκόπον: it is necessary to locate the horoscope (τὸν... ὡροσκόπον... ὁρίζειν δεῖ) with great precision (ἐξακριβούμενον). Wolf, the translator, understood it as an adverb: horoscopus autem ad regulam summa diligentia finiendus est; but the adjective does not exist. It would perhaps be better to think of an ἐξακριβωμένως (an adverb from a participle, like προηγουμένως and many others), even if undocumented.

[28] The American translator, to overcome the difficulty, provides proof of how a text can be distorted: in fact, instead of 'Seeing how many degrees (the Moon) is distant from the Sun,' he translates: “Seeing how many degrees of the Moon it [i.e. the dodekatemorion, presumably] has;” in other words, he changes the subject, which is no longer the Moon, but the dodekatemorion, and the genitive (τοῦ Ἡλίου) depending on ἀπέχει (... is from the Sun), becomes a subjective genitive, leaving the verb (ἀπέχει) all alone. But that would not be all... (cf. Porphyry the Philosopher, Introduction to the Tetrabiblos, transl. by J. H. Holden, Tempe AZ 32009, p. 29).

[29] Cf. CCAG VIII.3, p. 116.

[30] Cf. G. Bezza, Commento al primo libro della Tetrabiblos di Cl. Tolemeo, Milano 1990, p. 356 f. On the ground of this text, Bezza maintains that the dodekatemorion should be calculated according to its horary circle! In any case, the Reader should know that, despite some faults, this work by Bezza is a valuable tool for all those who deal with astrology, including professors.

[31] Cf. CCAG I, p. 154 f. Feraboli's comment is truly interesting (op. cit. p. 395): “Rhetorius, dedicating a chapter to the δωδεκατημόρια, shows that he has not understood the texts: he contrasts the system of Dorotheus and of Paul of Alexandria, and interprets the 2°30' of Ptolemy's passage (as well as—strangely—Porphyry, 19 [lege 39], source of Hephaestion, III 4,20) according to the criterion of the transfer of points of the planetary δωδεκατημόρια planetari; Rhetorius ignores the multiplication by 12 or by 13 and transfers the quantity in degrees of the planet directly onto the circumference, assigning 2°30' to each sign (18, in CCAG I, p. 154; cf. VIII 3, p. 116)." In our opinion, it is Feraboli the one who “shows that she has not understood the texts.” First of all, the scholar should have explained what she meant by “criterion of the transfer of points of the planetary δωδεκατημόρια;" secondly, Rhetorius—as the text we have translated demonstrates—is not at all ignorant of “the multiplication by 12 or by 13;” thirdly, it would have been necessary to exemplify how Rhetorius “transfers the quantity in degrees of the planet directly onto the circumference.” — It seems more useful to note that the expressions used by the author of this chapter attributed to Rhetorius are very different from those employed in the chapters where he explains how to find the aspects of the stars (cf. CCAG VIII.1, p. 223÷237), chapters which are not translated in the Compendium by James H. Holden (Tempe [AZ] 42009).

[32] The text, instead of the expression in use, as is also found in Paul, says to make the degrees of the star equal to 13, that is, make each degree equal to (παρά) 13, which recalls the παρά, mentioned in n. 21. To our knowledge, such an expression occurs only here.

[33] The text says having done.

[34] Cf. G. Pettinato, La scrittura celeste, Milano 1998, p. 125 e 298. An American scholar, Francesca Rochberg—who is familiar with Pettinato, citing him in her bibliography—had the audacity to publish a book with the same title (The Heavenly Writing, Cambridge 2004), in which, with a certain skill—which, however, can only appeal to fools—she surreptitiously passes off her schizophrenic opinions as revealed truth.

[35] There is hardly a single sentence in over 600 pages in which the author does not launch his satirical arrows against a doctrine of which he—despite his erudition and the vast literature he has consulted—has understood nothing and has wanted to understand nothing, since the sole purpose of his literary enterprise has been to submerge the entire astrological doctrine under a blaze of mocking cackles and sardonic sneers.

[36] Op. cit., p. 93, n. 2, where, however, the reference to Bouché-Leclercq's AG is incorrect.

[37] Cf. Manilio, op. cit., I, p. 346.

[38] Cf. M. Manilius, Astronomicon, recensuit et enarravit Alfred Ed. Housman, II, Londinii 1912, p. xxii ff. The editor also illustrates very clearly how such an absurdity arose.

[39] G. Bezza had already understood this (cf. Arcana mundi, Milano 1995, p. 540 n. 8), even if, later, in his Commentary (p. 356 ff.), regarding the twelfth, he performs acrobatic flights, affirming that in Francesco Turatello's chart the twelfth of the Moon falls at 12°07' Libra, but, if the natal Moon is in 2°18' Virgo, the dodekatemorion remains in Virgo (first column of the table) and the degree is = 2°18' × 12, that is 27°36' ♍.


[Dorno, December 10, 2025]


© Franco Luigi Viero

INDIETRO