Calcolo dodecatemorio.

Come si calcola il dodecatemorio.

Tra i papiri greci la più antica menzione dei dodecatemorî s'incontra in due oroscopi risalenti al sec. I: uno già pubblicato con traduzione e commento in GH;[1] l'altro rinvenuto ad Ossirico.[2] In ambito letterario le prime attestazioni dei dodecatemorî si trovano in Manilio[3] e in Manetone.[4]

In P. Lond. 130 sono dati i dodecatemorî del Sole, che si trova a 14° Ariete, e della Luna, posta a 13° Toro. Secondo l'estensore dell'oroscopo sia il dodecatemorio del Sole sia quello della Luna cadono in Scorpione. Gli autori di GH, invece, i quali dànno la loro (errata) procedura di calcolo a p. 6, ritengono che i due dodecatemorî dovrebbero cadere in Bilancia: a 2° quello del Sole e a 19° quello della Luna. Nel commento astrologico (p. 25) scrivono: «Si deve presumere un grossolano errore nel calcolo del dodecatemorio». A nostro parere non si tratta d'errore, ma di una errata interpretazione di come vada eseguito il calcolo, cosicché non si tien conto del segno in cui si trova l'astro, ma del successivo.[4*] Il risultato è comunque sbagliato, ma non è un errore. — In P. Oxy. 2555, si dànno i dodecatemorii di Luna (a 19°+½+¹/3+¹/12[5] = 19°55' Capricorno), Sole (a 29°+½+¹/3+¹/12 = 29°55' Toro), Saturno (a 2°10' Capricorno) e Giove (a 23°30' Cancro). Ebbene i rispettivi dodecatemorî sono posti in Leone, Ariete, Capricorno e Ariete: tutti corretti.

Manilio è il più antico autore ad informare che il dodecatemorio è un segmento d'eclittica di 2°30' e che ogni segno ne contiene 12: «Rivolgi ora la tua attenzione a un elemento minore a vedersi, ma di gran peso e che si lascia designare solo con un termine greco, dodecatemorio, definizione che si spiega da sé. Infatti, dato che i segni (sidera) hanno tutti trenta gradi, [sott. e sono dodici,] all'inverso il numero (30) vien suddiviso per due volte sei; l'operazione stessa fa risultare che in (dette) sezioni vi sono due gradi e mezzo».[6] È quanto basta in questa sede, perché, se proseguissimo, dovremmo riempire molte pagine per discutere i molti versi di Manilio incompresi e mal tradotti. — Manetone, di poco posteriore a Manilio,[7] non fornisce alcun calcolo del dodecatemorio, ma in cinque occasioni ne descrive il necessario coinvolgimento.[8]

Prima di illustrare il calcolo del dodecatemorio, pare opportuno citare alcuni testi che ne trattano, a cominciare dal capitoletto, in cui Tolemeo ne fa rapida menzione:[9]

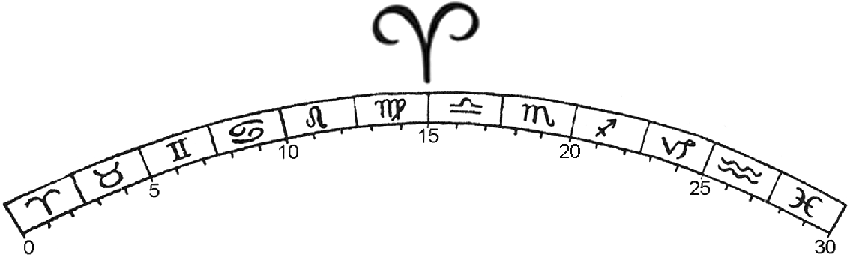
1. Alcuni hanno distribuito le reggenze (οἰκοδεσποτεῖαι) in settori ancor più minuti rispetto a questi (appena esposti), chiamandoli 'luoghi' e 'gradi', ed assumendo come 'luogo' il dodicesimo del dodicesimo, vale a dire 2 gradi e mezzo, ed assegnandone la signoria (κυρεία) ai segni in successione. Altri, poi, per giunta secondo differenti criteri di collocazione non razionali (κατ’ἄλλας τινὰς ἀλόγους τάξεις), hanno attribuito ciascun 'grado', sempre dall'inizio (del segno), a ciascuno degli astri, conformemente alla collocazione delle circoscrizioni (ὅρια) dei Caldei. 2. Ebbene, questo tipo di suddivisione (τοῦτο μὲν οὖν), basandosi su un ragionamento fallace e non naturale, lo metteremo da parte; quello, invece ((ἐκεῖνο δέ), risultando degno d'attenzione, lo prenderemo in considerazione, poiché è ragionevole istituire quali inizi dei dodecatemori e delle circoscrizioni i segni solstiziali e quelli equinoziali, e questo è stato in certa misura chiarito da chi ne ha scritto prima di noi, e soprattutto (è ragionevole) perché osserviamo che le loro nature (φύσεις), potestà (δυνάμεις) e coreggenze (συνοικειώσεις) hanno origine, in base a quanto già spiegato, dagli inizi dei tropici e degli equinozi e non da altro, quale che sia. 3. Ponendo altri inizi, o saremo costretti nelle previsioni a non considerare affatto le loro nature, oppure, considerandole, fallire, avendo violato e alterato le distanze dello zodiaco che conferiscono ad essi le potestà loro proprie.

Questa è la nostra traduzione del testo a noi giunto. Dobbiamo aggiungere, affinché il nostro Lettore ne sia informato, che le traduzioni in italiano più accreditate, ossia quella della Feraboli, preferita dagli accademici, e quella del Bezza, differiscono.[10] Il problema non è irrilevante.

In questo capitoletto Tolemeo conferma (1) d'essere a conoscenza del dodecatemorio di 2 gradi e ½, e (2) che esso è attribuito a un segno secondo l'ordine dei segni. Ma, siccome la suddivisione descritta subito dopo – quella riguardante i singoli gradi, la cosiddetta monomoiria – è ἄλογον, cioè una trovata illogica, va rimarcato che questa di 2 gradi e mezzo non è definita tale.[11] Il periodo che segue, contiene una contrapposizione (τοῦτο[12] μὲν... ἐκεῖνο δέ) del tutto ignorata dai traduttori. Ricordiamo che Tolemeo ama molto queste particelle e non le adopera mai a caso. Di qui, τοῦτο μὲν si riferisce a quanto immediatamente precede, cioè alla suddivisione ridotta al singolo grado, ἐκεῖνο δέ alla suddivisione per dodecatemorî. Dopodiché Tolemeo sembra alludere allo scollamento tra zodiaco siderale e zodiaco tropico. Lasciando perdere la questione della precessione degli equinozi, chiediamoci piuttosto, perché Tolemeo ne acceenni proprio qui e non nel cap. 10 (Delle stagioni dell'anno)! Le traduzioni del Robbins (London 1940), dunque, e della Feraboli sono zoppe e, quindi, errate. Tolemeo intende dire che, se le circoscrizioni, che egli riferisce per scrupolo,[13] e i dodecatemorî non fossero inquadrati – come i segni del resto, ma non lo dice – entro i solstizi e gli equinozi, si sgretolerebbero miseramente e diverrebbero del tutto inutili all'arte della previsione. Chi siano, poi, questi «alcuni (τινες)» che introdussero il dodecatemorio, l'astronomo non dice.

Di tutt'altro avviso si dimostra il Commentatore anonimo, il quale peraltro fornisce dettagli non ricavabili dal testo tolemaico, tanto da dare l'impressione a bella prima che egli legga un testo diverso:[14]

Ottimo è quel didatta che riferisce non solo i principi veri e giusti, ma discute anche quelli falsi che possono fuorviare la mente di un giovane; ebbene, tale s'è dimostrato il vetusto (Tolemeo) nell'insegnamento relativo alle circoscrizioni, confutando le false opinioni degli Egiziani. Ed ora egli vuole confutare altri loro principi che mirano alla vanità. Oltre alla suddivisione dei segni in circoscrizioni, vi erano presso gli Egizi anche altre suddivisioni minori, quali quella dei dodecatemorî e dei singoli gradi. Affinché uno non pensi che egli voglia trascurarle, ne scrive per confutarle in quanto fatue e miranti alla sola vanagloria.[15] Vi erano dunque presso di loro siffatti dodecatemorî: ciascun grado occupato da un astro, lo moltiplicavano per dodici; a ciascun segno assegnavano 30 gradi (sottraendoli dal totale) e dove terminasse (il resto), dicevano che quello era il dodecatemorio. Così fa anche Doroteo.[16] Egli, però, non fa (la moltiplicazione) per dodici, ma dice che a ciascun segno assegnava 2 gradi e ½ e, dove andava a finire, diceva che quello era il dodecatemorio. Dice(, alla fin fine,) la stessa cosa di Doroteo.[17] In effeti i 2 gradi e ½ sono analoghi al numero 30. Se facciamo 2 × 12, risulterà il numero 24, ma i 12 semigradi aggiunti completano il numero 30. Che (i due computi) concordino, si prendano i (primi) tre gradi dell'Ariete, come dice Doroteo,[18] e, secondo Tolemeo, si diano 2½ all'Ariete.[19] Il mezzo grado sarà del Toro, e sarà il grado 6.[20] Ed il risultato è lo stesso con entrambi i metodi.

Ciò che il Commentatore anonimo vuol dire si può spiegare come segue: sia che si moltiplichino i gradi per 12 e poi si sottraggano tante volte 30° quante è possibile, sia che si divida il segno in settori di 2 gradi e ½ e si controlli in qual settore finisca, il risultato è il medesimo. Infatti, 3° Ariete × 12 = 36°, tolgo 30°, e restano 6° che cadono nel secondo segno a partire dall'Ariete, cioè il Toro. Oppure, dividendo il segno in settori di 2 gradi e mezzo, rilevo che 3° cadono nel secondo settore: 3° - 2°30' = 30' che, moltiplicati per 12, dànno 6° del secondo settore attribuito al Toro.

Nel successivo scolio intitolato Della monomoiria (Περὶ μονομοιρίας), cui invero dedica poche righe, il Commentatore anonimo riprende a parlare del dodecatemorio e ripete quanto già detto: «Chiamavano così i dodecatemorî in conseguenza della ripartizione (per 12): dividendo infatti trenta gradi zodiacali per 12, davano a ciascun segno 2 gradi e ½; tale è, in effetti, l'ampiezza della dodicesima parte». A questo punto il testo mostra d'essere il risultato di un rimpasto corrotto, annunciato peraltro dalle contraddizioni precedenti. La nostra traduzione cerca di rendere le inconguenze sintattiche del testo: «Altri (astrologi) d'un tempo (παλαιοί) per il numero 12 * i 5 moltiplicarono, il che è lo stesso dei 2° gradi e ½. Se infatti aggiungi il numero assommatto dei gradi, completi i 30° del dodecatemorio. (Tolemeo) s'è preso gioco del dodecatemorio ed ha dimostrato, avendo spezzettato in (parti) più minute, di 2 particelle (μορίων) e mezzo, di tale ampiezza infatti risulta il dodicesimo della particella, che quelli d'un tempo per maggior chiarezza moltiplicavano per 12». È evidente che quest'ultima parte, sconclusionata com'è, è il risultato di un rimpasto maldestro.[21]

Secondo l'Anonimo, poi, Tolemeo dimostra «false tutte (queste) cose che gli Egiziani approvano; esse, infatti, non sono né credibili, né naturali, cioè non sono vere, anche se possono sembrare verosimili.[22] E nemmeno vuole riferire la nuda tradizione dei dodecatemorî, ma ad essa unisce un necessario piccolo postulato (θεωρημάτιον), questo: gli inizi di quel che si osserva nello zodiaco, dice, ha di necessità il suo inizio o dai tropici o dagli equinozi: tutto quello, infatti, che è già stato dimostrato a questo riguardo, l'abbiamo riferito, e principalmente testimoniano detti inizi gli astrologi che ci hanno preceduto (οἱ παλαιοί)». Segue un'ultima considerazione: «Da quanto sopra quelli che hanno ben riflettuto sui dodecatemorî, controbattono con sagacia: se troviamo allora che il dodecatemorio dell'Ariete è caduto in Vergine, o lo usiamo o non lo usiamo. Se non lo usiamo, è stato preso come inutile sovrappiù; se lo usiamo, non potremo più comprendere la potestà dell'Ariete, come era stata compresa fin dall'inizio».

Questo è quanto il Commentatore anonimo dedica al dodecatemorio. Nonostante la disastrosa condizione del testo, possiamo rilevare quanto segue: egli è convinto che Tolemeo ritenga assurdi anche i dodecatemorî, e non solo l'assegnazione ai pianeti del dominio su ogni singolo grado; ma non è quello che si legge nel testo tolemaico. Che poi Tolemeo si prenda gioco dei dodecatemorî (διέπαιξε), è una gratuita opinione. Che gli autori di una tale suddivisione siano gli Egizi, è dato per scontato; ma non è quello che leggiamo. Sorprende che «il vetusto (ὁ παλαιός)» sia Tolemeo – e che si tratti di Tolemeo è confermato dall'attribuire a lui la confutazione delle circoscrizioni egizie. Gli scoli del Commentatore anonimo sono di norma preceduti dalla citazione di una frase od espressione del testo tolemaico; il citato scolio sulla monomiria è titolato, appunto, Περὶ μονομοιρίας, ma il vocabolo non ricorre mai in Tolemeo. Tutto ciò, senza tralasciare l'evidente rimpasto di due redazioni, alimenta il sospetto che qualcun altro abbia messo mano al commento dell'Anonimo, stravolgendo e ampliando il testo originario. Diversamente, saremmo costretti a supporre che il testo tolemaico di questo capitoletto ci sarebbe giunto mutilo e corrotto. Possiamo, in ogni caso, ammettere, che il calcolo del dodecatemorio sia opera dello scrupoloso Commentatore anonimo, che lo illustra forse in contrapposizione con altri procedimenti errati, come quello di Paolo Alessandrino, imprudentemente accreditato da Neugebauer e van Hoesen.[23]

Un secondo testo, per il quale gli studiosi mostrano interesse, è il capitoletto Del dodecatemorio di Porfirio:[24]

Il dodecatemorio della Luna si coglie in due modi. In primo luogo, avendo osservato quanti gradi detiene la Luna nel segno, da quel segno dividi (i suoi gradi) per 2½ in successione e, dove termina il numero, quello sarà il dodecatemorio. Se, ad es., la Luna detiene il grado 13 dell'Ariete, darò all'Ariete 2½, al Toro 2½, ai Gemelli 2½, al Cancro 2½, al Leone 2½, e dunque il dodecatemorio finirà in Vergine, domicilio di Mercurio. Similmente, il dodecatemorio del Sole si coglie allo stesso modo, come pure quello dell'oroscopo: quando infatti osservi qual grado sorga, dividerai per 2½ quelli che stanno per sorgere.[25]
Alcuni colgono il dodecatemorio della Luna altrimenti. Visto quanti gradi dista dal Sole, da questi sottrai le trentine (possibili), i restanti gradi <dividili> per 2½, a partire dal segno che la Luna detiene (τὰς δὲ λοιπὰς <ἐπιμέριζε> ἀνὰ βL΄, ἀφ’ οὗ ἂν ἐπέχηται ἡ Σελήνη ζῳδίου).[26] Se non vi sono trentine, dividi quei gradi per 2½. L'oroscopo, però, va definito con molta precisione (ἐξακριβουμένους) ricorrendo alle tavole.[27]

Nella prima parte, Porfirio, che non pare amare molto i calcoli, dà la giusta procedura. Nella seconda, invece, senza dichiararne la fonte e senza offrire un esempio, riserva al dodecatemorio della Luna un trattamento speciale, che si può semplificare come segue: ai gradi del Sole si sommino i gradi tra la Luna e la fine del segno (se il risultato supera i 30° gradi, si sottraggano); quindi si divida il resto per 2½°, e dove termina il numero, lì è il dodecatemorio della Luna. In pratica, con questo metodo si sposta la Luna dal suo grado iniziale, il che sia sotto l'aspetto astronomico che astrologico, non ha senso. In astrologia, infatti, nessuna legge o figura può sussistere senza avere un riscontro, anche solo per analogia, con le apparenze. A nostro avviso, Porfirio, o non ha capito la sua fonte, oppure il testo ha subito un rimaneggiamento incauto,[28] com'è rilevabile dall'ultima frase sull'oroscopo, del tutto fuori contesto. La Feraboli, di contro, fidandosi degli editori, non segnala alcuna difficoltà. Comunque sia, Porfirio conferma il corretto calcolo.

Insieme con questo di Porfirio si cita, presumibilmente a conferma, il 23^mo capitoletto tratto dal Riassunto (Συγκεφαλαίωσις) del primo libro delle Nozioni preliminari (Εἰσαγωγικά) di Antioco. Vale la pena proporre anche il testo greco:

κγ'. Καὶ τὸ δωδεκατημόριον δὲ τῆς Σελήνης διχῶς θηρεύεσθαί φησιν, ὅπως τε δεῖ τὸ κλίμα λαμβάνειν κα̥ὶ ὡς τὰ μὲν ὀρθὰ τῶν ζῳδίων ἐν πλείονι, τὰ δὲ πλάγια ἐν ἐλάσσονι ἀναφέρεται.[29]

Il solo a tradurlo, a nostra conoscenza, è il Bezza: «In due modi si prende il dodicesimo della Luna, in quanto si deve osservare la latitudine: infatti, i segni retti ascendono in maggior tempo, i segni curvi in minor tempo».[30] Una resa che oltraggia tanto il buonsenso quanto la lingua greca. La nostra traduzione suona diversamente:

23. E (Antioco) dice [= spiega] che il dodecatemorio della Luna si scova in due modi, e (dice) come occorre assumere il clima, e che [= perché] i segni retti ascendono in maggior tempo, mentre quelli obliqui in minor tempo.

Qui, l'epitomatore si limita semplicemente a riferire il contenuto del capitolo 23. In altre parole, non v'è nulla che riguardi il dodecatemorio, se non la citazione del vocabolo.

Chiudiamo la carrellata con un testo attribuito a Retorio, ancorché la lingua lasci dubbiosi:[31]

18. Dei dodecatemorî degli astri.
Gli antichi esposero i dodecatemorî dei gradi degli astri in tre modi: Paolo nella sua Introduzione ha detto di moltiplicare i gradi dell'astro per 13[32] e dal suo segno cedere 30 gradi per segno, e, dove arriva il numero, in quel segno è il dodecatemorio dell'astro. Doroteo nell'11^mo libro dice di moltiplicare i gradi per 12. Tolemeo dice nel 26^mo capitolo del primo libro di cedere due (gradi) e mezzo (ad ogni segno) lungo il segno (stesso). Io per esperienza ho trovato il metodo di Doroteo più concordante con quello di Tolemeo; e mi trovo più d'accordo con questi (due) metodi, cioè quello del 12 e quello del 2½; così infatti i due metodi arrivano allo stesso segno, come in quest'esempio: la Luna si trova a 25° Toro; moltiplicato[33] questo 12 volte, trovo 300 gradi, che libero a gruppi di 30 per volta a partire dal Toro, e si finisce a 30° Acquario a completamento dei segni. Oppure, liberati questi 25° Toro a gruppi di 2½ per volta, (il computo) finisce in Acquario a completamento del segno di due gradi e mezzo. Se facessi 25 per 13 il numero finirebbe a 25° Pesci e sarebbe una grossa differenza. Nelle geniture il metodo dei dodecatemorî è cosa necessaria: di questi ho dato anche gli esiti (che essi segnalano), affinché qualcuno non ne faccia uso come se fosse solo un sovrappiù.

Anche qui è confermato il calcolo che più sotto illustriamo. Tornando a Tolemeo, chi sono questi alcuni? Oggi sappiamo, grazie alla pubblicazione di alcune tavolette in scrittura cuneiforme, che il dodecatemorio proviene direttamente dagli astrologi mesopotamici, cioè dai Caldei![34] Perché Tolemeo, che pure nomina i Caldei, attribuisca i dodecatemori genericamente ad “alcuni”, è quanto meno strano. Forse, non volendo attribuirne la paternità a quegli stessi, di cui aveva più sopra contestato le circoscrizioni – anche se in misura minore rispetto a quelle degli Egizi –, preferì restare nel vago. Ma è solo un'ipotesi priva di alcun sostegno. Chi non volesse ammettere la dipendenza dell'astrologia egizia da quella caldea, dovrebbe giocofcorza ipotizzare una fonte comune con ovvie conseguenze temporali.

E veniamo, finalmente, al calcolo dei dodecatemorî. La tavoletta tradotta dal Pettinato (v. nota 34) non lascia alcun dubbio: «Trenta giorni corrispondono a un beru (= 30°). Tu devi prendere 2,5 giorni come una porzione, e così otterrai 12 porzioni della costellazione dell'Ariete. Moltiplica 2°30' per 12 che costituiscono il nucleo della costellazione dell'Ariete e così arrivi a 30° come risultato. In 30 giorni si hanno 12 segmenti della costellazione dell'Ariete. I segmento: il suo nome è Ariete; II segmento: il suo nome è Toro; [ecc.]. Totale: 12 segmenti della costellazione di Ariete nel mezzo della quale tragittano il Sole e la Luna. Io te l'ho indicato». È chiaramente il didatta che istruisce l'allievo su come suddividere i restanti segni zodiacali per completare l'intero circolo di 360°.

Abbiamo preparato la tabella qui sotto, seguendo esattamente le istruzioni dell'astrologo mesopotamico. I numeri romani della prima riga numerano le colonne e i segmenti corrispondenti, mentre nella seconda riga sono indicati i gradi iniziali e finali di ogni singolo segmento.

Nella prima colonna, invece, sono elencati tutti i segni dall'Ariete ai Pesci. Siccome i dodecatemorî di ciascun segno iniziano, come dice la tavoletta, dal segno stesso, ad ogni segno indicato nella prima colonna seguono, nell'ordine e sulla stessa riga, tutti gli altri segni.

Iniziamo con l'esempio dato dal Commentatore anonimo: 3° Ariete. Ebbene, dalla seconda riga rileviamo che il terzo grado cade nella seconda colonna. Sulla riga che inizia dall'Ariete, la casella relativa della seconda colonna appartiene al Toro, che è il segno ove cade il dodecatemorio di 3° Ariete. Semplicissimo! Quanto ai gradi dobbiamo moltiplicare 3° × 12 = 36°, ed il trentaseiesimo grado a partire da 0° Ariete corrisponde a 6° Toro. Ma facciamo un secondo esempio: 11° Vergine. L'undicesimo grado cade nella V colonna, scendiamo fino ad incrociare la casella della riga che inizia con la Vergine, e troveremo il Capricorno, che è il segno dove cade il dodecatemorio di 11° Vergine. Quanto ai gradi moltiplichiamo 11° × 12 = 132°, ed il centotrendaduesimo grado a partire da 0° Vergine corrisponde a 12° Capricorno (150 + 132 = 282); come controprova: 11° × 360° : 30° = 132°.

La bislacca distinzione fra 'dodecatemorî zodiacali' e 'dodecatemorî planetari' è stata causata dall'incomprensione dei testi, e dalla propaganda fatta da Bouché-Leclercq, autore del famoso L'Astrologie Grecque (1899), da tutti ammirato e citato, il cui pretenzioso titolo dovrebbe essere in realtà (Comment ridiculiser) l'astrologie grecque (en la traitant à ma façon).[35] Detta distinzione fra i due tipi di dodecatemorî è ribadita e dalla Baccani[36] e dalla Feraboli.[37] Il solo che abbia ben compreso il problema è lo Housman: «Non consiglio ad alcuno di leggere il resoconto sull'argomento fatto da Bouché-Leclercq, l'astrol. Grecque pp. 299-303, a meno che non voglia essere confuso e raggirato».[38]

Tornando al calcolo, il solo caso dubbio si ha quando il risultato raggiunge esattamente i confini dei settori. L'esempio citato da Retorio con la Luna a 25° Toro cade a fagiuolo: 300°, infatti, senza primi né secondi, possono significare 30° Acquario come pure 0° Pesci; un caso non impossibile, ma molto improbabile.

Concludendo, il principio su cui si basa il dodecatemorio è dato da una semplicissima analogia:[39] come 30° stanno a 360°, così il dodecatemorio sta a 30°; infatti 30 × 30 : 360 = 2,5. La prova della giustezza del dodecatemorio si ha – come abbiamo visto – moltiplicando i gradi nel segno × 360, e dividendo il risultato per 30: esso dev'essere uguale ai gradi nel segno × 12. Qualsiasi altro calcolo è da considerarsi un errore.

Detta analogia, poi, ne fa scaturire un'altra: come la Luna in 1 mese (30 giorni) percorre tutto lo zodiaco (mediamente 2 giorni e mezzo, 2°30' × 12, per segno), allo stesso modo il Sole in 1 mese passa in rassegna i 12 dodecatemorî di un segno, cioè l'intero (micro-)zodiaco.

NOTE.

[1] Cf. O. Neugebauer e H.B. van Hoesen, Greek Horoscopes, Philadelphia 1987, cf. p. 21 ss. (P. Lond. 130).

[2] Cf. P. Oxy. XXXI (1966) nr. 2555, p. 83 ss., riproposto anche in Donata Baccani, Oroscopi greci, Messina 1992, p. 81 ss., senza traduzione.

[3] Cf. Astr. 2,713÷722 [Housman]. Sull'edizione italiana di Manilio (Milano 1996) converrà stendere un velo pietoso (si salvano solo, ma non del tutto, i contributi della Feraboli). Utilizzabile e sincera è quella curata da Dora Liuzzi in cinque volumi (Lecce 1995÷1997).

[4] Cf. Apotel. 4,165 ss.: Ταῦτα μὲν ὡράων σκεπτήρια· νῦν δέ με χρειὼ | ἀκτινηβολίας ὁρίων τ' αἰθωπὰ κέλευθα | δωδεκατημορίων τ' ἄστρων κυκλόεσσαν ἐνισπεῖν | Ζῳδιακήν... La traduzione dell'editrice (Jane L. Piè-leggièro [Oxford 2023]) è la seguente: «These signs are from the Hours. Now I'll describe Castings of rays, the shining paths of terms, And, of the twelve parts of the stars, the round Zodiacal path», ove of the twelve parts of the stars avrà un senso solo nella testa della traduttrice. Manetone intende: «Queste sono le cose da considerare al momento della nascita; ma ora è opportuno che io spieghi l'irraggiamento, l'oscuro procedere delle circoscrizioni ed il ripetersi ciclico dei dodecatemorî nello zodiaco...». Mentre fino al v. 164 Manetone ha parlato degli effetti delle varie configurazioni «su coloro che nascon mortali (γεινομένοις θνητοῖσιν)... nell'ora della nascita (ἐς βίου ὥρην)» (v. 17), che la filologa mal traduce, dal v. 165 egli intende spiegare l'effetto degli aspetti (l'irraggiamento), delle circoscrizioni e dei dodecatemorî. Siccome dei segni ha già parlato, l'abbinamento con le circoscrizioni esclude che Manetone con δωδεκατημόριον intendesse 'segno zodiacale'. Il procedere delle circoscrizioni non può essere scintillante, perché esse non si vedono: αἶθοψ è connesso etimologicamente con αἴθω, ardo, αἰθός, scuro, bruno, arso, αἰθίοπες, dal viso scuro, αἰθαλόω, annerisco, ecc. Quanto poi all'espressione δωδεκατημόρια (τῶν) ἄστρων, si legga quel che scrive lo Housman in Manil. Astr. II, p. xxiv.

[4*] Dodici secoli dopo, Giovanni Camatero nella sua Introductio in astronomiam – un poema astrologico in versi redatto in un greco tardo disseminato di espressioni del linguaggio parlato, in taluni casi di non immediata comprensione (ed. Weigl, Leipzig 1908) – propone un bizzarro calcolo, in cui il segno del dodecatemorio si trova partendo dal segno successivo: «Sia la Luna in Ariete a 15 gradi; moltiplica il luogo del grado – dodici (per) quindici fa centottanta – badando ai dodici segni prima che ai gradi e da' a ciascun segno in sequenza 30°, e [= ma] 15° vanno riservati al segno della Luna, poiché la Luna, posizionata a 15° Ariete, abbisogna di (altri) 15° per compoletare i 30° dell'Ariete. Per questo motivo non si comincia dall'Ariete, ma dal Toro: da' (quindi) 30° al Toro, similmente ai Gemelli, al Cancro e al Leone, ed egualmente ai rimanenti, (cioè) 30° alla Vergine; quanto alla Bilancia (li dài) in questo modo: (i gradi computati) raggiungono in Bilancia il 15esimo grado. Dove i gradi conteggiati della Luna (αἱ τῆς Σελήνης ψῆφοι) giungono alla fine, fa' conto che è lì il dodecatemorio» (cf. vv. 3003÷3019). Secondo Camatero, dunque, per trovare il segno, una volta moltiplicati i gradi della Luna per 12, si assegnano 30° a ciascun segno, iniziando dal segno successivo: 180° equivalgono a 6 segni ed il sesto segno a partire dal Toro è la Bilancia; quanto al grado, siccome alla Luna mancano 15° per completare l'Ariete, si tolgono dalla Bilancia e si troverà così che il dodecatemorio cade in 15° Bilancia. Altro esempio: Luna a 17° Toro; 17 × 12 = 204, corrispondenti a 6 segni + 24°; il sesto segno a partire dai Gemelli è lo Scorpione; siccome, però, alla Luna mancano 13° per completare il Toro, essi vanno sottratti ai 24°, onde il dodecatemorio della Luna posta a 17° Toro, cade in 11° Scorpione. Il computo è errato, ma, come nel caso di P. Lond. 130, deriva da un fraintendimento, cioè dal non aver compreso il principio sotteso.

[5] Questa è la nostra lettura dell'ultima frazione; l'editore e la Baccani leggono ι’β’, che non ha senso. Invero, lo iota sembra avere un apice, ma deve trattarsi d'una svista; infatti la frazione andrebbe letta ¹/10+2! Questo papiro è verosimilmente la bella copia degli appunti originali scritti da chi redasse l'oroscopo. Lo si può desumere dalla posizione dei luminari, che, pur avendo gradi diversi, avrebbero i medesimi primi; le frazioni di grado, infatti, sono le medesime, il che è altamente improbabile. Una 'coincidenza', dunque, da ascrivere al copista.

[6] Cf. Manil. Astr. 2,693÷699.

[7] Alla fine del sesto libro (v. 745 ss.) Manetone fornisce i dati del suo cielo di nascita, ed è talmente chiaro e preciso che si può datare con facilità: egli nacque il 27 o il 28 maggio dell'a. 80, data gregoriana. Resta l'incertezza del luogo e dell'ora esatta. Infatti, se il MC si trovava in Sagittario (βέλος Κένταυρος ἀνέλκων) e l'ascendente in Acquario, supponendo la nascita ad Alessandria, il 27 maggio la nascita si colloca tra le 23^h24^m e le 0^h13^m (ora locale, LMT), cioè fra l'entrata del MC in Sagittario e l'uscita dell'ascendente dall'Acquario; il 28 maggio, invece, tra le 23^h20^m e le 0^h09^m. Ovviamente, le posizioni dei pianeti sono quelle siderali; noi abbiamo usato quelle secondo Lahiri, perché sono sempre le più prossime alle posizioni date dagli astrologi ellenistici, e spesso coincidono. Gli autori di GH (v. p. 92), poi, confondono il Sagittario con la costellazione del Centauro; e, siccome è astronomicamente impossibile, se l'ascendente è in Acquario, che il MC cada in Bilancia, da studiosi che hanno fatto proprio l'atteggiamento tipico dello studioso americano, spostano l'ascendente in Capricorno, cioè attribuiscono a Manetone il loro errore. Persino la Piè-leggièro ha capito che la costellazione non c'entra! Considerazioni astrologiche, infine, che rimandiamo ad altra sede, inducono a ritenere che la data da preferire sia il 28 maggio.

[8] Cf. Apotel. 4,209.227.250.298.336.

[9] Cf. Tetr. 1,22.

[10] Laddove la Feraboli, ad es. (cf. Cl. Tolomeo, Le previsioni astrologiche, Milano ⁴1998, p. 90), traduce «è ragionevole infatti far coincidere l'inizio dei segni con i punti equinoziali e solstiziali», il Bezza (cf. Commento al primo libro della Tetrabiblos, Milano 1990, p. 351) rende «è infatti conforme alla ragione assumere gli inizi dei dodecatemori e dei confini a partire dai punti equinoziali e solstiziali». Ciò dipende in parte dall'omissione di καὶ τὰς τῶν ὁρίων (e quelli delle circoscrizioni) nei codd. del gruppo α (la Feraboli in apparato fa confusione) accolta dal Robbins (London 1940) e dalla Feraboli che lo copia. Infatti, senza ὁρίων il precedente δωδεκατημορίων può essere inteso come 'dei segni (zodiacali)', mentre l'abbinamento con ὁρίων imporrebbe, dato il contesto, d'intendere 'dei dodecatemori'. Lo Hübner (Teubner 1998, p. 82) in apparato ammette d'ignorare se detta omissione sia corretta o no.

[11] Disturba un poco quel «chiamandoli luoghi (τόπους... ὀνομάσαντες)», giacché non risulta da alcuna altra fonte che i 'dodicesimi dei dodicesimi' fossero chiamati 'luoghi'.

[12] Gli editori leggono ταῦτα, poiché τοῦτο è dato dal solo codice V, il più autorevole; non che la diversa lezione cambi molto, ma l'attenzione posta da Tolemeo in queste correlazioni ci fa preferire τοῦτο.

[13] Le circoscrizioni attribuite a Tolemeo, infatti, non sono le sue, bensì di un anonimo, trovate – dice l'Astronomo – in un consunto manuale, e ne parla perché sono più coerenti sia delle circoscrizioni egizie sia di quelle caldee.

[14] Cf. In Claudii Prolemæi Quadripartitum enarrator ignoti nominis, ed. Hieronymus Vuolfius, Basileæ 1559, p. 47 s. Sulla questione di chi sia il traduttore, cf. il dettagliato articolo di St. Heilen, H. Zäh, Who Edited and Who translated the Anonymous Commentary to Ptolemy's Tetrabiblos and (Ps.-)Prophyry's Isagoge (Basel 1559)?, in “MHNH” 20 (2020), pp. 93-128.

[15] Il testo tolemaico non allude minimamente alla vanagloria: Tolemeo si limita a dire che la suddivisione per singoli gradi è illogica.

[16] Cf. Doroth. p. 327, vv. 7÷9 [Pingree], ove però la testimonianza del Commentatore anonimo è citata solo a metà! Oltre a quella del Commentatore anonimo vi è anche la testimonianza di Retorio (cf. CCAG I, p. 154, v. infra), il quale cita le tre diverse procedure di calcolo utilizzate dagli astrologi d'un tempo (παλαιοί), tra cui quella, a nostro avviso errata, esposta da Paolo Alessandrino (cf. Elementa apotelesmatica, p. 45 s. [Boer]) e ripetuta dal suo commentatore Eliodoro (cf. In Paulum Alex. Commentarium, p. 38 s. [Boer], ora attribuito a Olimpiodoro). Efestione, quanto alla procedura di calcolo, se la sbriga in quattro parole (cf. Heph. Theb., Apotelesmatica, p. 42 [Pingree]); altrove (p. 234,8 ss.; II, p. 1,20; 47,5; 268,26) ribadisce con la medesima frase l'importanza che ai fini della previsione gli antichi attribuivano al dodecatemorio dell'oroscopo.

[17] Abbiamo tradotto questo periodo secondo il testo greco del Wolf, ma è chiaramente pasticciato e contraddittorio. Un lieve miglioramento si avrebbe espungendo la frase «Dice la stessa cosa di Doroteo (ταὐτὸ δὲ φησὶ τῷ Δωροθέῳ)», che ripete quella più sopra: «Così fa anche Doroteo».

[18] Cioè, moltiplicali per 12 e togli 30.

[19] Qui il Commentatore sta dicendo il contrario di quel che ha detto poco prima.

[20] Cioè, moltiplica la differenza di ½ grado × 12.

[21] Il testo ha παρὰ τὸν δώδεκα ἀριθμὸν (per il numero 12), seguito da i 5 moltiplicarono, che traduce un corrotto ἐπολλασίασαν, anziché ἐπολλαπλασίασαν. Ma in greco moltiplico per si dice πολυπλασιάζω (meno bene πολλαπλασιάζω) ἐπί o εἰς, mentre divido per si dice μερίζω παρά. Nella frase, però, non v'è nessuna traccia di μερίζω, né παρὰ τὸν δώδεκα ἀριθμόν (per il numero 12) può essere retto da ἐπολλαπλασίασαν. Tentare di raggiustare il testo senza l'ausilio dei codici manoscritti non avrebbe alcun senso. Dobbiamo, pertanto, attendere l'edizione critica che lo spagnolo Caballero-Sánchez sta preparando.

[22] La traduzione di quest'ultima frase è piuttosto libera, perché il testo è contorto.

[23] V. GH, p. 6.

[24] Cf. Porphyrii philosophi Introductio in Tetrabiblum Ptolemaei, edd. Aem. Boer et St. Weinstock, in CCAG V.4, p. 210 s.

[25] Porfirio intende dire che, se l'oroscopo è a 23° Acquario, vanno divisi i 23 gradi che stanno per sorgere, non certo quelli che sono già sorti!

[26] Si legga ἀπὸ τοῦ ζῳδίου, οὗ [da ὃ per assimilazione] δ’ ἂν ἐπέχηται ἡ Σ.

[27] Che valore desse l'editore ad ἐξακριβουμένους (i codd. hanno ἐξακριβωμένους, che non cambia nulla), accusativo plurale del participio presente medio, non sapremmo immaginare; tirato per i capelli, uno potrebbe pensare, ad un ἐξακριβούμενον come predicato di ὡροσκόπον: occorre fissare l'oroscopo (τὸν... ὡροσκόπον... ὁρίζειν δεῖ) preciso preciso (ἐξακριβούμενον). Wolf, il traduttore, lo ha inteso come un avverbio: horoscopus autem ad regulam summa diligentia finiendus est; ma l'aggettivo non esiste. Sarebbe forse meglio pensare ad un ἐξακριβωμένως (avverbio da participio, come προηγουμένως e molti altri), ancorché non documentato.

[28] Il traduttore americano, per superare la difficoltà, fornisce la prova di come si possa stravolgere un testo: infatti, invece che Visto quanti gradi (la Luna) dista dal Sole, traduce: «Seeing how many degrees of the Moon it has (Vedendo quanti gradi della Luna esso [il dodecatemorio, presumibilmente] ha)»; in altre parole cambia il soggetto, che non è più la Luna, ma il dodecatemorio, ed il genitivo (τοῦ Ἡλίου) dipendente da ἀπέχει (dista dal Sole), diventa un genitivo soggettivo, lasciando il verbo (ἀπέχει) solo soletto. Ma non sarebbe finita qui... (cf. Porphyry the Philosopher, Introduction to the Tetrabiblos, transl. by J. H. Holden, Tempe AZ ³2009, p. 29).

[29] Cf. CCAG VIII.3, p. 116.

[30] Cf. G. Bezza, Commento al primo libro della Tetrabiblos di Cl. Tolemeo, Milano 1990, p. 356 s. Partendo da questo testo, il Bezza sostiene che il dodecatemorio va calcolato secondo il suo circolo orario! In ogni caso il Lettore sappia che, a parte talune pecche, questo lavoro del Bezza è uno strumento prezioso per tutti coloro che si occujpano di astrologia, accademici compresi.

[31] Cf. CCAG I, p. 154 s. Interessante davvero il commento della Feraboli (op. cit. p. 395): «Retorio, dedicando un capitolo ai δωδεκατημόρια, mostra di non aver compreso i testi: contrappone il sistema di Doroteo e di Paolo Alessandrino, e interpreta i 2°30' del passo di Tolomeo (come pure – stranamente – Porfirio, 19 [lege 39], fonte di Efestione, III 4,20) secondo il criterio del trasferimento di punti dei δωδεκατημόρια planetari; Retorio ignora la moltiplicazione per 12 o per 13 e trasferisce direttamente sulla circonferenza la quantità in gradi del pianeta, assegnando 2°30' ad ogni segno (18, in CCAG I, p. 154; cf. VIII 3, p. 116)». A nostro parere è la Feraboli che «mostra di non aver compreso i testi». Innanzitutto, la studiosa avrebbe dovuto spiegare che cosa intendesse per «criterio del trasferimento di punti dei δωδεκατημόρια planetari»; in secondo luogo, Retorio – come dimostra il testo da noi tradotto – non ignora affatto «la moltiplicazione per 12 o per 13»; terzo, sarebbe stato necessario esemplificare come Retorio «trasferisce direttamente sulla circonferenza la quantità in gradi del pianeta». — Pare più utile osservare che le espressioni usate dall'autore di questo capitoletto attribuito a Retorio sono molto diverse da quelle impiegate nei capitoletti ove spiega come trovare gli aspetti degli astri (cf. CCAG VIII.1, p. 223÷237), capitoli peraltro non tradotti nel Compendium curato da James H. Holden (Tempe [AZ] ⁴2009).

[32] Il testo invece della locuzione in uso, com'è anche in Paolo, dice far uguali i gradi dell'astro a 13, cioè ogni grado fallo diventare uguale a (παρά) 13, il che ricorda il παρά, di cui alla n. 21. A nostra conoscenza una tale espressione ricorre solo qui.

[33] Il testo dice avendo fatto.

[34] Cf. G. Pettinato, La scrittura celeste, Milano 1998, p. 125 e 298. Una studiosa americana, Francesca Rochberg – la quale pur conosce il Pettinato, perché lo cita nella bibliografia –, ha avuto l'impudenza di pubblicare un libro con lo stesso titolo (The Heavenly Writing, Cambridge 2004), ove con una qualche abilità – che peraltro può far presa solo sui gonzi – fa surrettiziamente passare le sue schizofreniche opinioni come verità rivelata.

[35] Non v'è quasi una sola frase in oltre 600 pagine, in cui l'autore non lanci i suoi strali satirici contro una dottrina, di cui egli – a dispetto dell'erudizione e della vasta letteratura consultata – non ha capito nulla e di cui non ha voluto capire nulla, dacché il solo scopo della sua impresa letteraria è stato quello di sommergere l'intera dottrina astrologica sotto un tripudio di cachinni beffardi e sardonici sogghigni.

[36] Op. cit., p. 93, n. 2, ove peraltro il riferimento all'AG di Bouché-Leclercq è errato.

[37] Cf. Manilio, op. cit., I, p. 346.

[38] Cf. M. Manilius, Astronomicon, recensuit et enarravit Alfred Ed. Housman, II, Londinii 1912, p. xxii ss. L'editore illustra altresì con molta chiarezza come abbia avuto origine una tale assurdità.

[39] L'aveva già compreso G. Bezza (cf. Arcana mundi, Milano 1995, p. 540 n. 8), anche se,poi, nel suo Commento (p. 356 ss.), a proposito del dodicesimo, si esibisce in acrobatici voli pindarici, affermando che nel tema di Francesco Turatello il dodicesimo della Luna cade a 12°07' Bilancia, ma, se la Luna natale si trova in 2°18' Vergine, il dodecatemorio resta in Vergine (prima colonna della tavola) ed il grado è = 2°18' × 12, ossia 27°36' ♍.

[Dorno, 10 dicembre 2025]

INDIETRO